CryptoHack [crypto] Modular Exponentiation / Public Keys
2024. 12. 3. 01:17ㆍWARGAME/CryptoHack
320x100
Modular Exponentiation
모듈러 지수 연산 문제입니다.

RSA의 모든 연산은 모듈러 지수 연산을 포함한다.
모듈러 지수 연산은 암호학에서 광범위하게 사용되는 연산으로, 보통 다음과 같이 표현된다 : 2^10 mod 17
이는 어떤 숫자를 특정 지수만큼 제곱한 후(2^10 = 1024), 다른 숫자로 나눈 나머지를 구하는 작업(1024 mod 17 = 4)으로 생각할 수 있다. python에서는 이 작업을 수행하는 내장 연산자인 pow(base, exponent, modulus)를 제공한다.
RSA에서는 모듈러 지수 연산과 소인수분해 문제를 활용하여 trapdoor function을 만든다. 이 함수는 한 방향으로는 쉽게 계산할 수 있지만, 올바른 정보를 가지고 있지 않으면 역으로 계산하기 어렵다. 이러한 특성을 이용해 메시지를 암호화하며, 키를 가진 사람만이 역연산을 통해 복호화할 수 있다.
플래그를 얻으려면 101^17 mod 22663의 답을 찾아라.
이 문제는 단순 계산으로 계산기를 이용해 풀 수 있다.
하지만 나는 암호학+파이썬 코드 공부를 위해 문제를 푸는 것이기 때문에!!
파이썬 코드를 사용해 계산을 해보자^^
pow(base, exponent, modulus) == (base)^(exponent) mod (modulus)
pow(101, 17, 22663)
가볍게 플래그 획득~~
위 문제가 너무 기초 문제라서.. 바로 다음 문제 풀이를 함께 하겠습니다 ㅎㅎ
Public Keys
공개키를 이용한 RSA 문제입니다.

RSA 암호화는 메시지를 지수 e와 모듈러스 N을 사용하여 모듈러 지수 연산을 수행하는 방식이다.
여기서 N은 보통 두 개의 소수 p와 q의 곱으로 정의된다. : N = p * q
지수와 모듈러스는 함께 RSA 공개키(N, e)를 형성한다. 가장 일반적으로 사용되는 e 값은 0x10001 또는 65537이다.
지수 e=65537과 소수 p=17, q=23을 사용하여 숫자 12를 암호화하라. 암호문으로 생기는 숫자는 무엇인가?
base == 12
exponent == 65537
modulus == N=p*q 이다.
그래서 python으로 표현하면~~
e=65537
p=17
q=23
N=p*q
print(pow(12,e,N))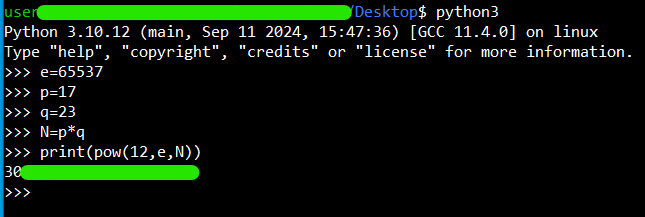
320x100
320x100
'WARGAME > CryptoHack' 카테고리의 다른 글
| CryptoHack [crypto] Favourite byte (0) | 2024.11.18 |
|---|---|
| CryptoHack [crypto] XOR Properties (0) | 2024.11.17 |